En el siguiente ejemplo se va a realizar un ejercicio de aplicación de derivadas, donde se buscara las dimensiones maximas que debería tener un cilindro que se inscribe en una esfera. Para ello se aplicarán tanto el criterio de la primera derivada comno el de la segunda a fin de hacer más completo el ejercicio.
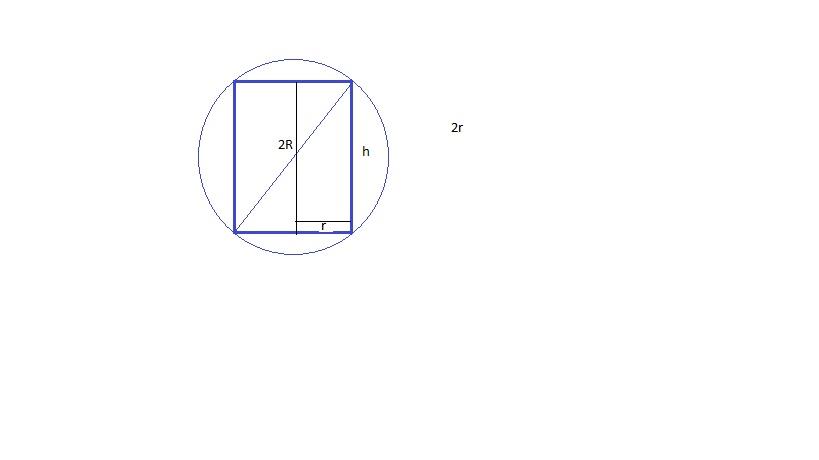
Hallar el cilindro de máximo volumen que puede inscribirse en una esfera de diametro 2R.
Solución:
Sea D = 2R . por tanto de la relación geometrica se tiene
4R^2 = 4r^2 + h^2
r^2 = (R^2-h^2/4) el volumen de un cilindro circular recto viene dado por la siguiente expresión
v = pi r^2 h, es decir, v = pi (R^2-h^2/4) h = pi (R^2 h- h^3/4)
esta es la expresión del volumen inscrito de un cilindro dentro de una esfera en función de la altura del mismo. ahora se deriva el volumen en función de la altura.
dv/dh = pi (R^2 - 3/4 h^2), igualando a cero la primera derivada se tiene:
R^2 = 3/4 h^2, tal que h = 2 * 3^(1/2) * R/3
aplicando el critrio de la segunda derivada par saber si el punto crítico es un máximo o mínimo
d^2V/dh^2 = -3/2 h, es negativo el signo, por tanto exite un maximo en el valor dado, el cual será
Vmax = 4*3^(1/2)*pi/9 * R^3. Rta.